深度学习全息原理 揭秘张量网络

深度学习的惊人效果背后隐藏着一个源自物理学的深刻原理——全息原理。这一原理最初在理论物理学中被提出，描述了高维时空中的信息可以完全编码在低维边界上的现象。令人惊讶的是，深度神经网络似乎采用了类似的机制，通过张量网络结构实现了对高维数据的高效表示与处理。

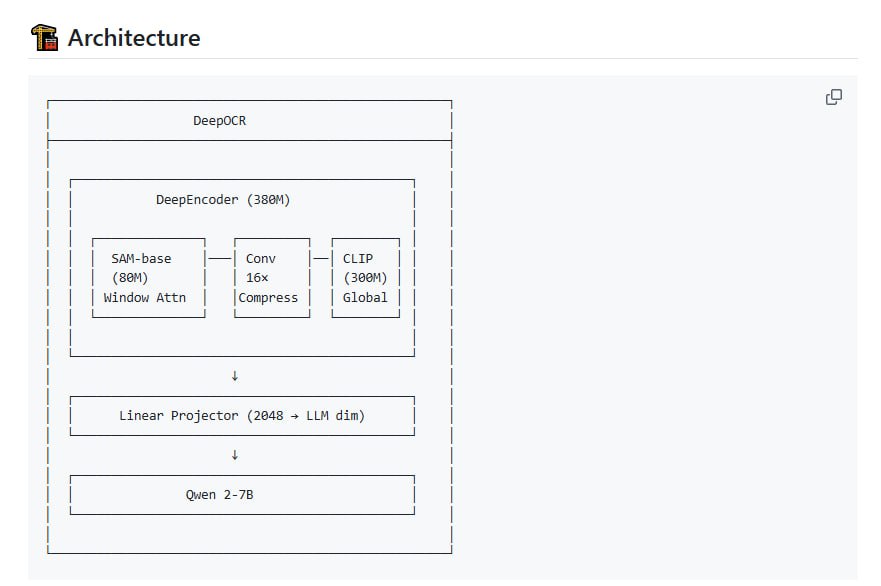
在深度学习的框架中，张量网络扮演着核心角色。张量可以被视为多维数组的推广，从简单的标量、向量到复杂的多维矩阵，构成了数据表示的基础。这种多层次、多维度的数据结构使得神经网络能够以紧凑的形式存储和操作海量信息。特别值得注意的是，张量网络通过巧妙的分组和分解策略，将复杂的计算任务拆解为多个简单操作的组合，大大提高了计算效率。

张量乘积与缩并操作构成了神经网络中信息融合与特征提取的数学基础。在神经网络的前向传播过程中，输入数据经过层层变换，实际上就是一系列张量运算的连续应用。每个网络层都可以看作是一个张量变换，通过线性或非线性操作将输入数据映射到新的表示空间。这种层层递进的处理方式，使得网络能够从原始数据中逐步抽象出越来越复杂的特征表示。

深度学习模型通过张量网络实现的高维数据压缩映射，与全息图记录三维场景到二维介质的过程有着惊人的相似性。这种结构不仅显著降低了计算复杂度，还增强了模型的泛化能力。当网络在训练过程中调整张量参数时，实际上是在学习如何最优地将高维数据投影到低维表示空间，同时保留最重要的信息特征。

这一视角为我们理解深度学习的工作机制提供了全新的见解。深度学习不仅仅是简单的层级堆叠，而是一个精心设计的信息编码与解码系统。通过全息式的信息处理方式，神经网络能够从看似无关的数据点中提取出有意义的模式，并在新的场景中准确地重建这些模式。这种对信息结构的“全息”把握，正是深度学习强大能力的源泉。

观看相关视频可以更直观地理解这些概念，视频中详细演示了张量网络在深度学习中的具体应用。

---

原文链接：深度学习为何有效？——全息原理揭秘